Jak powstało życie?

PODZIAŁ KOMÓRKI

a) Podział genetycznie niekontrolowany (część twórcza)

Z zasad geometrii wiemy, że powierzchnia (S) jest proporcjonalna i wzrasta proporcjonalnie do kwadratu wymiarów liniowych (a). Objętość (V) natomiast jest w taki sposób powiązana z sześcianem wymiarów liniowych. Kiedy zwiększymy dwukrotnie długość boku kwadratu, jego powierzchnia wzrośnie 22 = 4 razy. Podwojenie długości boków sześcianu sprawi, że jego objętość wzrośnie 23 = 8 razy. Możemy więc napisać:

S ~ a^2 , V ~ a^3

W jakiej relacji pozostają jednak S i V ? Przekształćmy powyższe wzory:

a ~ V^1/3 → S ~ V^2/3

Interesujące będzie zbadanie jak ze wzrostem objętości zmienia się stosunek: S/V. Podzielmy wzór:

S ~ V^2/3 przez V

S/V ~ V^-1/3 → S/V = m V^-1/3 , m - wsp.proporcjonalności

Jedną z takich funkcji przedstawia wykres 1:


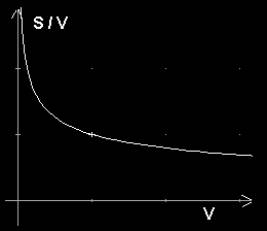
Wykres 1. Funkcja S/V = m V^-1/3 dla m = 1.


Jest to funkcja malejąca. Wraz ze wzrostem argumentu V maleje wartość S/V.
Kiedy komórka (którą przedstawimy abstrakcyjnie za pomocą kuli) dzieli się, to powstają dwie komórki potomne o objętości v = 0,5 V.

Wzory na ich objętość wyglądają następująco:

V = 4/3 π R^3 komórka macierzysta
v = 4/3 π r^3 komórka potomna

Można łatwo obliczyć, że promienie tych kul pozostają w relacji: R = r 2^1/3.

Jak wynika z wykresu 1, wraz ze wzrostem objętości maleje stosunek powierzchni do objętości, z czego wynika, że powierzchnia rośnie wolniej niż objętość.

Komórka, mająca 2 razy większą objętość, nie będzie miała 2 razy większej powierzchni. Wzory naszych komórek na powierzchnię wyglądają następująco:

P = 4 π R^2 = 4 π (r 2^1/3 )^2 = 4 π r^2 2^2/3 komórka macierzysta
p = 4 π r^2 komórka potomna

Można zauważyć, że P < 2p, bo 2^2/3 < 2

Zróbmy teraz realne założenie, że prymitywny składnik błony komórkowej T produkowany jest w cytoplazmie, całą objętością komórki. Z tego wniosek, że powierzchnia chemotonu będzie wzrastać proporcjonalnie do jego objętości według wzoru:

S ~ V, S = kV, k - wsp. proporcjonalności

Powierzchnia chemotonu ma konkretną postać:

Sch = k 4/3 π R^3
Sch = k 4/3 π R^3 = k 4/3 π r^3 (2^1/3)^3 = 2 k 4/3 π r^3

Postawmy teraz warunek podziału: Sch = 2p, czyli:

2 k 4/3 π r^3 = 8 π r^2 → r = 3/k , R = 3/k 2^1/3

Gdy prakomórka osiągnie promień R równy 3/k 2^1/3, będzie miała 2 razy większą objętość i 2 razy więcej materiału na powierzchnię, niż komórka potomna. Proces podziału będzie więc wtedy możliwy. I nigdzie nie musi być zapisywany!

b) Rozdział materiału genetycznego

Załóżmy że na początku istnieją tylko 4 rodzaje cząstek RNA i są one dla komórki niezbędne. Niekoniecznie replikują się one w tym samym tempie. Komórka dzieli się i są one losowo rozdzielane do komórek potomnych. Jakie są tu zagrożenia? Liczba kopii RNA, będących niezależnymi cząsteczkami nie jest zsynchronizowana. Niektóre mogą dzielić się szybciej – inne wyraźnie wolniej. Poza tym z przyczyn czysto losowych komórka potomna może nie otrzymać wszystkich czterech rodzajów cząstek.

Problemy te rozwiązuje związanie ze sobą wszystkich czterech cząstek na jedną, czterogenową nić. Wtedy to na pewno wszystkie cztery geny trafią do komórki potomnej i będą replikowane wolniej (są na dłuższej cząstce), ale w takiej samej liczbie kopii. Te korzyści zwyciężyły (problem 10). I dlatego powstały chromosomy – długie nici DNA z zapisanymi w nich sekwencjami wielu genów.