Ewolucja człowieka czyli dziecinna małpa

WIELCY SPALAJĄ SIĘ WOLNIEJ

Jak już wiemy, wraz ze wzrostem objętości maleje wartość stosunku powierzchnia / objętość. Produkcja ciepła zachodzi prawie we wszystkich komórkach organizmu, jest więc proporcjonalna do jego objętości. Ilość ciepła wypromieniowywana zależy natomiast od wielkości powierzchni ciała. Pamiętamy, że powierzchnia rośnie wolniej niż objętość wraz ze wzrostem wymiarów liniowych.

Same rozważania jakościowe nasuwają więc już podejrzenie, że przy wzroście objętości ciała, a co za tym idzie ilości produkowanej energii cieplnej, wzrost powierzchni nie będzie wystarczający do usunięcia jej z organizmu. Prowadziłoby to do jej kumulacji w organizmie i – w konsekwencji – przegrzania. Organizmy większe muszą więc produkować mniej ciepła na jednostkę objętości, niż organizmy małe.

Zilustrujmy powyższe rozważanie za pomocą ścisłego, abstrakcyjnego modelu.

Weźmy 2 sześciany. Jeden o boku a, drugi o boku 10a (patrz rys.4.). Objętość małego sześcianu będzie zatem równa 1/1000 objętości dużego.

Załóżmy teraz że mały sześcian traci ciepło w ilości Q / 8 na każdą ścianę na jednostkę czasu.

Ilość traconego wtedy ciepła na jednostkę objętości wynosi więc: (8 x Q/8) / a^3 = Q / a^3

Zauważmy, że niewielka ilość małych sześcianów wypełniających duży ma część wspólną z jego powierzchnią. Każdy z nich wydziela energię, lecz nie każdy może uczestniczyć w jej oddawaniu na zewnątrz. Większość znajdująca się wewnątrz traci tyle ciepła, ile zyskuje. Strata netto wynosi więc dla nich O (patrz rys.4.).

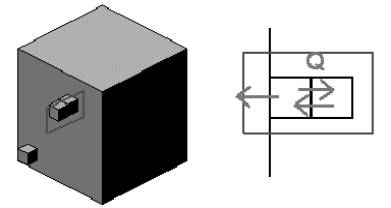
Rys.4. Dwa rodzaje sześcianów, których boki pozostają w stosunku 1 : 10. Po prawej pokazane jest powiększenie przekroju dwóch małych sześcianów, z których tylko jeden graniczy ze ścianą dużego.

Tutaj ilość ciepła traconego na jednostkę objętości wynosi: (8 x Q/8 x 100) / 1000 a^3 = Q /10a^3 w jedn.czasu.

Duży sześcian potrzebowałby 10x więcej czasu, żeby ilość ciepła oddanego na jednostkę objętości, była równa tej dla małego sześcianu . Jednak w tym czasie powstawałyby nowe porcje energii cieplnej. Jego „komórki” są więc zmuszone obniżyć tempo metabolizmu. Długość życia zależy bezpośrednio od tego tempa w sposób malejący, ono zaś – jak pokazałem – zależy od objętości, czy przy realnym założeniu stałej gęstości tkanek – od masy, również w sposób malejący. I to dlatego duże zwierzęta żyją dłużej!

ZAKOŃCZENIE

Chciałbym tutaj przytoczyć cytat z książki „Tak zwane zło”, wspomnianego już wcześniej noblisty - K. Lorenza. Cytat, który wydaje się stanowić credo autora:

"Wierzę krótko mówiąc w zwycięstwo prawdy. Wierzę, że wiedza o przyrodzie i jej prawach stanie się z czasem bardziej powszechnym dobrem ludzkości, co więcej, jestem przekonany że już dzisiaj jesteśmy na najlepszej drodze ku temu. Wierzę, że przyrost wiedzy przyniesie ludzkości w darze ideały prawdziwe, a rosnąca potęga humoru dopomoże jej do wyśmiania fałszywych".

Maciej Panczykowski


Artykuł pochodzi z Wortalu Nauk Przyrodniczych Autora: http://mpancz.webpark.pl
Dziękujemy za zgodę na publikację tekstu.